Не высчитывает тригонометрическую функцию

Всем доброго времени суток! Помогите разобраться или найти ошибку..

#include <iostream>
#include <cmath>

#define PI 3.14159265

using namespace std;

void main()
{
float a, z1, z2;
    cout << "Введите a: ";
    cin >> a;
    a= a *PI/180;
    z1 = (sin(2*a)+sin(5*a)-sin(3*a))/(cos(a)+1-2*pow(sin(2*a),2));
    z2 = 2*sin(a);
    cout << "z1= " << z1 << endl;
    cout << "z2= " << z2 << endl;
    system ("pause");
}

В итоге у меня выходит либо 0, либо z1=z2 при этом ответ совсем не верный. Помогите ребята.
Вот вообще мое условие:

Честно скажу, я плохо шарю в тригонометрии. Но вижу по моему одну ошибку. В конце первого примера в квадрате только синус, а у тебя в программе в квадрате «синус два альфа»

pow(sin(2*a),2)

попробуй написать

sin * sin(2*a)

что-то в этом роде, не знаю как правильно ))

или может

(pow(sin, 2) 2*a)

но точно скажу «синус в квадрате» и «синус два альфа в квадрате» это разные вещи

либо z1=z2 при этом ответ совсем не верный.

c чего Вы взяли? Посчитайте. Я вот посчитал и всё сошлось.

В конце первого примера в квадрате только синус, а у тебя в программе в квадрате «синус два альфа»

Всё там правильно.

Честно скажу, я плохо шарю в тригонометрии.

ага... судя по

sin * sin(2*a)
(pow(sin, 2) 2*a)

в плюсах и в математике ты тоже ни хрена не шаришь

Блин, ребзя, а тут что не так?

#include <iostream>
#include <cmath>

#define PI 3.14159265

using namespace std;

void main()
{
    setlocale(LC_ALL, ("russian"));
    float a, b, z1, z2;
    cout << "a: ";
    cin >> a;
    cout << "b: ";
    cin >> b;
    a = a *PI / 180;
    b = b *PI / 180;
    z1 = pow(cos(a) - cos(b)), 2) - pow(sin(a) - sin(b)), 2);
    z2 = (-4*pow(sin((a-b)/2),2))*cos(a+b);
    cout << "z1 = " << z1 << endl;
    cout << "z2 = " << z2 << endl;
    system("pause");
}

Вот условие:

Интересно, откуда у многих такая любовь к типу float? Экономия на спичках? С double оно вроде по любому сподручнее.

Скобки лишние убери

z1 = pow(cos(a) - cos(b), 2) - pow(sin(a) - sin(b), 2);

Интересно, откуда у многих такая любовь к типу float?

преподы сказали «флоать рулитъ»
при этом пишут так:

float x = 2.4 ;

))))

Интересно, откуда у многих такая любовь к типу float? Экономия на спичках? С double оно вроде по любому сподручнее.

В большинстве скриптовых языков, float — тип данных для любых чисел с плавающей запятой.
Те, кто начал изучать плюсы после PHP, JS, Python и т.п., могут по привычке его использовать.

В учебных примерах я не вижу особой разницы. Но если конкретная задача требует особой точности — тогда без double никуда.

А что такого плохого в float? Если диапазон принимаемых значений устраивает, зачем выделять 8 байт, туда где хватит 4? Типом int вы пользуетесь же и не смеётесь, на long long везде подряд не меняете!?

преподы сказали «флоать рулитъ»
при этом пишут так:
float x = 2.4 ;

Что здесь смешного? Зачем 8 байт под такое маленькое число?

Типом int вы пользуетесь же и не смеётесь, на long long везде подряд не меняете!?

хоть это и холиварная тема, но:

Since the 80x87 FPUs and 80486 CPU always convert single and double precision values to extended precision, extended precision arithmetic is actually faster than single or double precision. Therefore, the expected performance benefit of using the smaller formats is not present on these chips. However, when designing the Pentium/586 CPU, Intel redesigned the built-in floating point unit to better compete with RISC chips. Most RISC chips support a native 64 bit double precision format which is faster than Intel's extended precision format. Therefore, Intel provided native 64 bit operations on the Pentium to better compete against the RISC chips. Therefore, the double precision format is the fastest on the Pentium and later chips

Но, скорее всего скорость будет практически одинаковая.

Я очень сильно извиняюсь, но кто-нибудь может подсказать, почему у меня на выходе z1=z2, какие-бы значения я не писал..

А что такого плохого в float? Если диапазон принимаемых значений устраивает, зачем выделять 8 байт, туда где хватит 4? Типом int вы пользуетесь же и не смеётесь, на long long везде подряд не меняете!?

Плохого в float, конечно, ничего нет ))

Выделять 4 байта вместо 8 — экономия на спичках, по современным меркам. Но есть одно соображение в пользу 8 байт: в самый ответственный момент (например, «эффект генерала») не хватит либо точности, либо диапазона. На эти грабли, в глобальном смысле, наступали уже очень много раз. Например, целочисленное переполнение счётчиков: когда писали программу никому не могло прийти в голову, что 256 (или 32768, или 65536) — когда-то будет слишком мало. Или другой пример: IP4 vs IP6. Поэтому, если это не требует существенных затрат, соломку лучше подстелить заранее.

Далее, в C/C++ числовые литералы с плавающей точкой по умолчанию считаются типом double. Поэтому, для тех, кто не въехал, смысл прохода Croessmah по «преподавателям» не в том, что используется тип float, а в том, что правильная запись выглядит так:

float x = 2.4f;

Аналогично и тип int используется по умолчанию для целочисленных литералов. А на счёт использования более длинных целочисленных типов... Это сейчас размер int 4 байта, а во времена былые, когда int весил всего 2 байта, вопрос использования long вместо int был весьма актуален. Кстати и сейчас существуют различные компиляторы под различные (!) процессоры, а размер типа int в стандарте не определён.

Я очень сильно извиняюсь, но кто-нибудь может подсказать, почему у меня на выходе z1=z2, какие-бы значения я не писал.

mychernenko, а тебе совсем лениво хотя бы в Экселе просчитать твои исходные формулы? Я вот прикинул, и получилось, что для аргументов в диапазоне -PI/2..+PI/2 значения этих выражений равны с точностью до погрешности вычислений с плавающей точкой. Думаю, что если поднапрячься, то можно преобразовать одно выражение в другое чисто математическими методами.

А график для обеих функций получился таким:

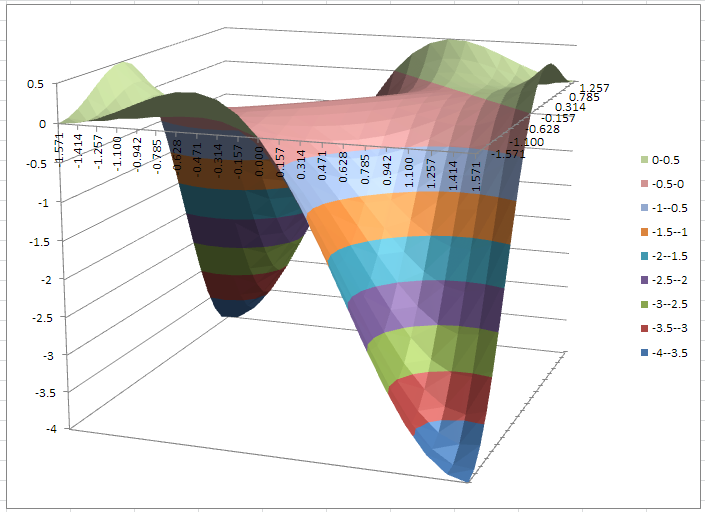
Cranium, я очень сильно Вам благодарен! Я считал на листке бумаги и видать где-то ошибся..